
Researchers can even restore other associational measures (such as risk differences) in the underlying cohort from each sampling design if auxiliary data on patients not selected as cases or controls are available. Note that none of the above interpretations of odds ratios requires a rare disease assumption. 1B), and the odds ratio in a risk set sampling (also called concurrent sampling) is equal to the rate ratio (or hazard ratio, according to analysis models) in the underlying cohort ( Fig. 1A), the odds ratio in a case-cohort sampling (also called inclusive sampling) is equal to the risk ratio in the underlying cohort ( Fig. Specifically, the exposure-outcome odds ratio in a cumulative incidence sampling (also called exclusive sampling) of controls is expectedly identical to the odds ratio in the underlying cohort ( Fig. Despite outcome-dependent sampling (which is also called “biased sampling”) that introduces selection bias, data collection only for cases and controls enables researchers to estimate some associational measures (such as risk ratio, odds ratio, and rate ratio) that would be obtained in an underlying cohort study, unless sampling depends on the exposure status in controls. In typical case-control studies, cases are all patients with an outcome in an underlying cohort, with multiple control selection strategies, as explained below. This paper aims to introduce basic principles of matching in case-control and cohort studies, with some recent examples.Ī case-control study is a design used to compare levels of exposures between cases and controls defined by the status of outcome of interest. In addition, in cohort studies, matching can remove or reduce confounding effects of matching factors.

Matching helps researchers reduce the volume of data for collection without much loss of information (i.e., improving cost efficiency) and obtain more precise estimates than simple random sampling of the same number of patients (i.e., improving statistical efficiency). The main purpose of matching is to increase study efficiency for data collection and subsequent statistical analysis. Matching is a technique by which patients with and without an outcome of interest (in case-control studies) or patients with and without an exposure of interest (in cohort studies) are sampled from an underlying cohort to have the same or similar distributions of characteristics such as age and sex. Matching is mainly used in observational studies, including case-control and cohort studies. If appropriately used, matching can improve study efficiency without introducing bias and could also present results that are more intuitive for clinicians. Propensity score matching is another matching method whereby patients with and without exposure are matched based on estimated propensity scores to receive exposure.
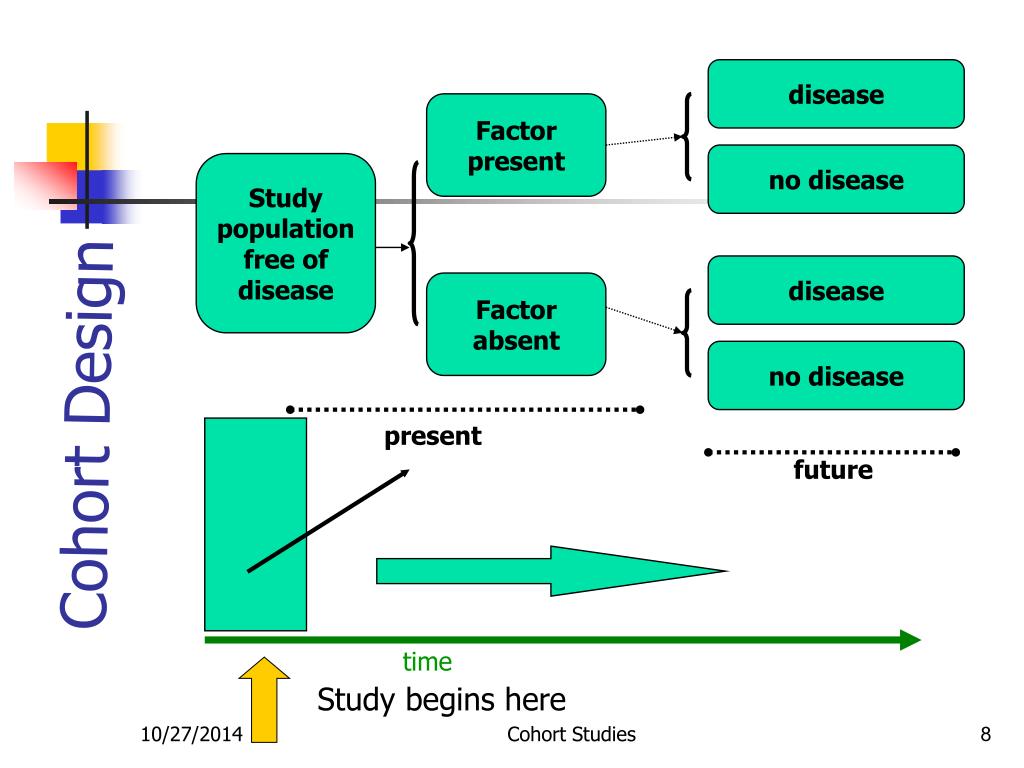
In cohort studies, exact matching is used to increase study efficiency and remove or reduce confounding effects of matching factors. In the statistical analysis of matched case-control studies, fixed-effect models such as the Mantel-Haenszel odds ratio estimator and conditional logistic regression model are needed to stratify matched case-control sets and remove selection bias artificially introduced by sampling controls. In case-control studies, besides time in risk set sampling, controls are often matched for each case with respect to important confounding factors, such as age and sex, and covariates with a large number of values or levels, such as area of residence (e.g., post code) and clinics/hospitals.

This technique is used to increase the statistical efficiency and cost efficiency of studies. Matching is a technique through which patients with and without an outcome of interest (in case-control studies) or patients with and without an exposure of interest (in cohort studies) are sampled from an underlying cohort to have the same or similar distributions of some characteristics.


 0 kommentar(er)
0 kommentar(er)
